Perceptron in C++ and Python
In this post, I’m going to cover the Perceptron Algorithm and compare its implementation in Python and C++.
Post Outline
Perceptron Explanation
The perceptron algorithm performs binary classifications by using a signed weighted sum of an input point to predict one of two output classes. The weights used are found by fitting a linear decision boundary to the training data. In order for the perceptron to achieve 100% accuracy, the data must be linearly separable. Formally, the perceptron prediction function f can be represented as:
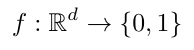
Predictions are made using the sign function as the activation function:
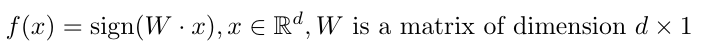
Training the perceptron is an iterative process. At a high level, the algorithm:
- Initialize weights to be zeroes
- For a predefined # of epochs
- makes a prediction for each misclassified point
- updates the weight vector
The update rule for the weight matrix is given by the following:
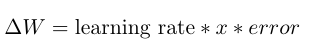
Error is calculated with the equation below where y is the label for each input x:
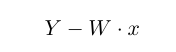
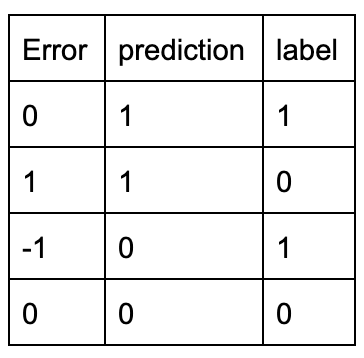
The intuition behind the error calculation is that the change applied to the weight matrix W will only be non zero for an incorrect classification. We can see this to be true from the table below:
Code
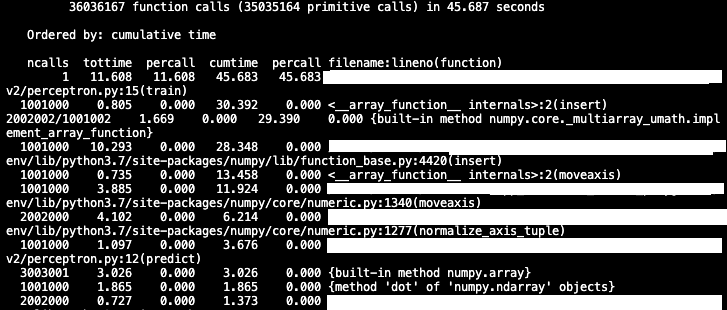
The code I wrote can be found here. Below is the code for a single iteration in the train method in both C++ and Python. From the code snippets, we can see see the similarities in the implementations and the differences in the syntax.
C++

Python

I use numpy in Python and Eigen (used by Tensorflow) in C++ to perform matrix operations. The C++ code is bound to Python using pybind11 (used by PyTorch), making it callable from Python. To make the code easier to compare, I implemented a class based approach in both C++ and Python. Both classes have the same functions down to the function signature. When writing the makefile, I used the -O3 flag to reduce execution time.
While the pseudocode included above has a learning rate variable, it is actually not necessary. In the perceptron algorithm, the learning rate only scales the weight matrix but does not actually change the sign of the prediction. Therefore, all the figures in the next section use a learning rate of 1. We can see this from the graph below, which shows there to be no correlation between accuracy and learning rate.
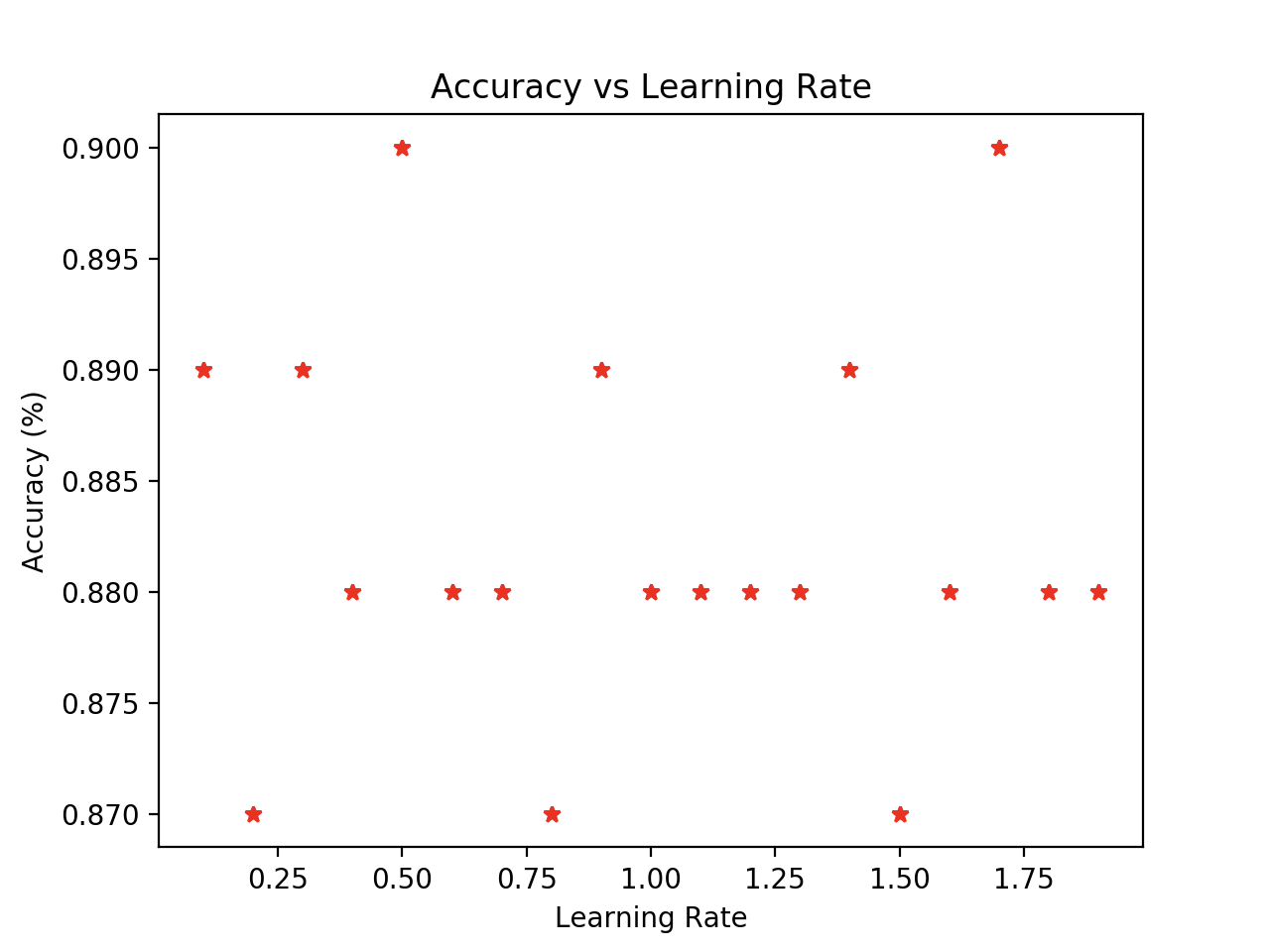
I chose to use this data source as it is 2d and can thus be visualized easily.
Benchmark Comparisons
Accuracy vs Epoch
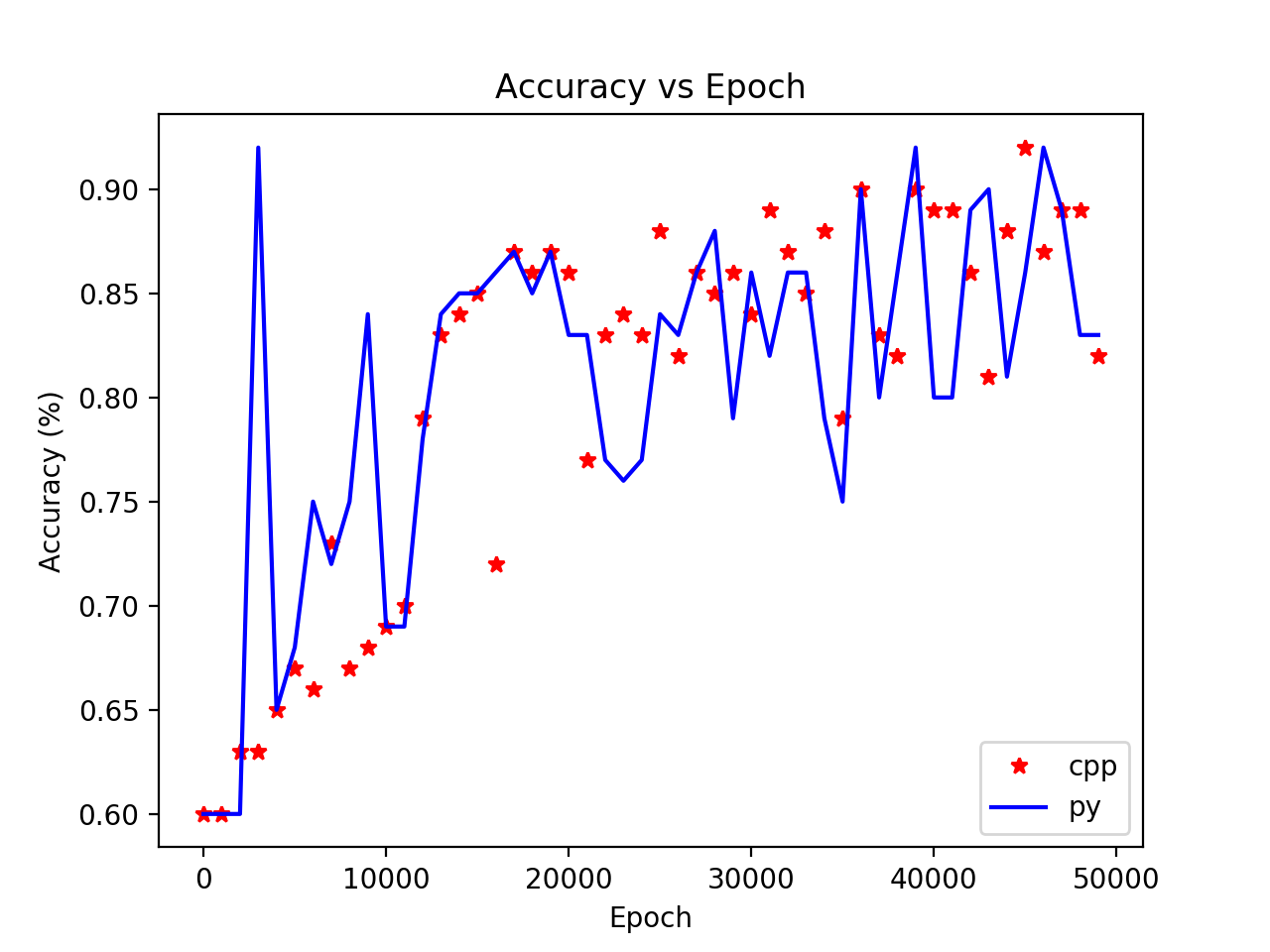
From the graph above, we can see that the C++ and Python accuracies vary equally as the number of epochs is increased (makes sense as they are the same algorithm so more of a sanity check).
Time vs Epoch
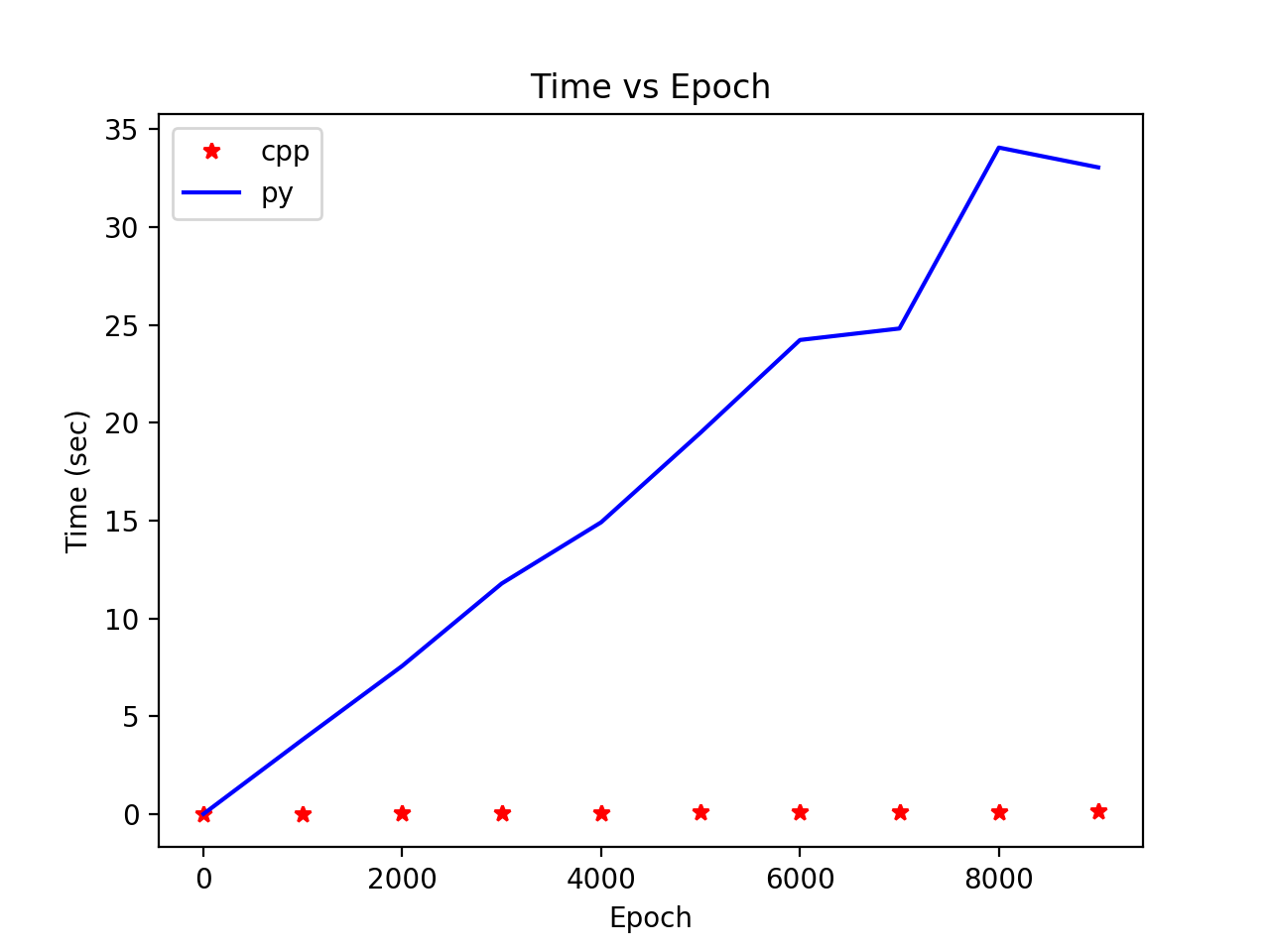
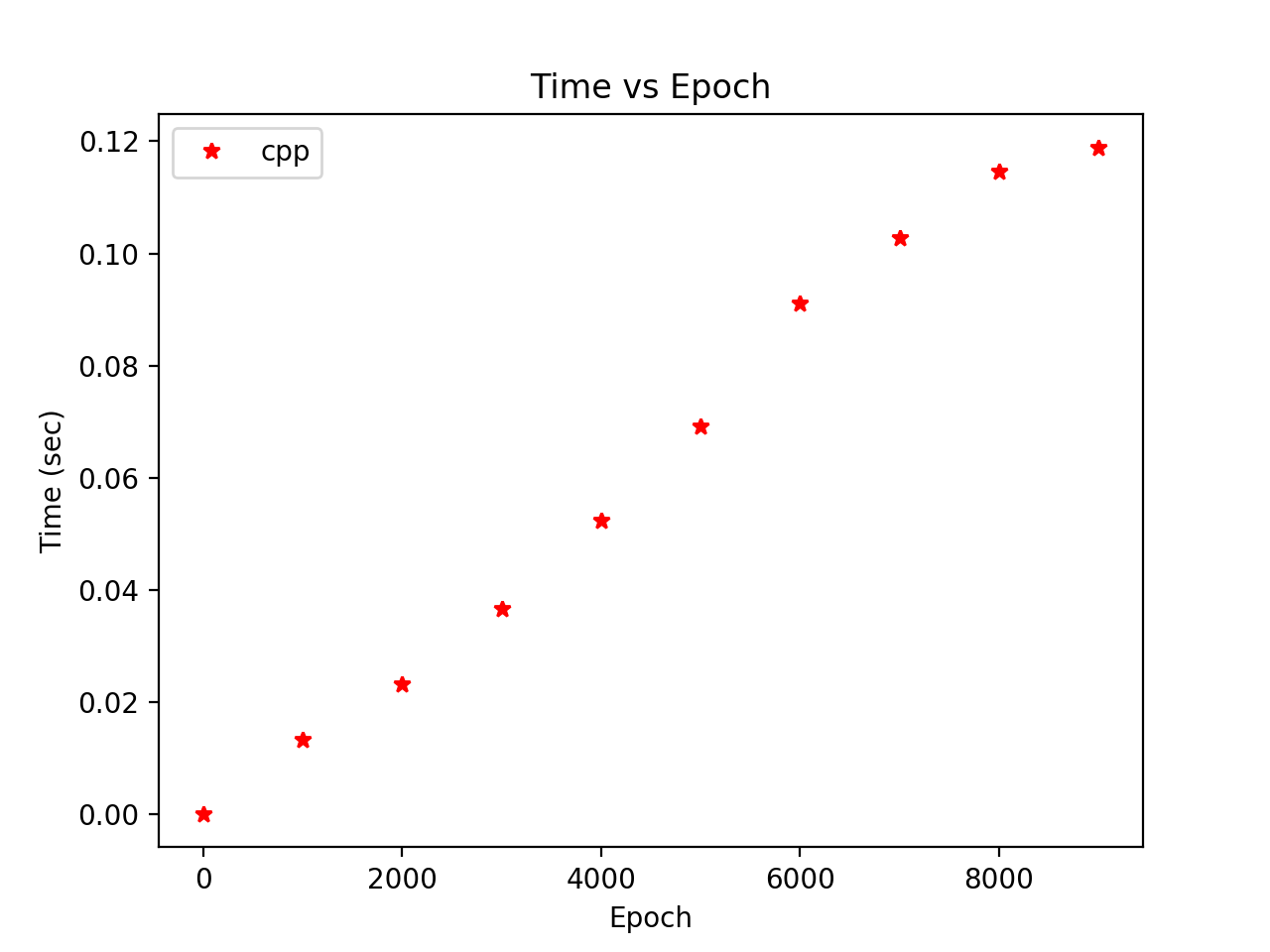
We can see from the figure on the left that the Python implementation takes much more time than the C++ implementation. The figure on the right is included to show that the C++ implementation’s time does increase with the number of epochs, albeit at a slower rate than the Python implementation.
Decision Boundaries
The next 6 figures show both the C++ and the Python implementations’ decision boundaries at increasing epochs.
Decision Boundary at 1000 Epochs
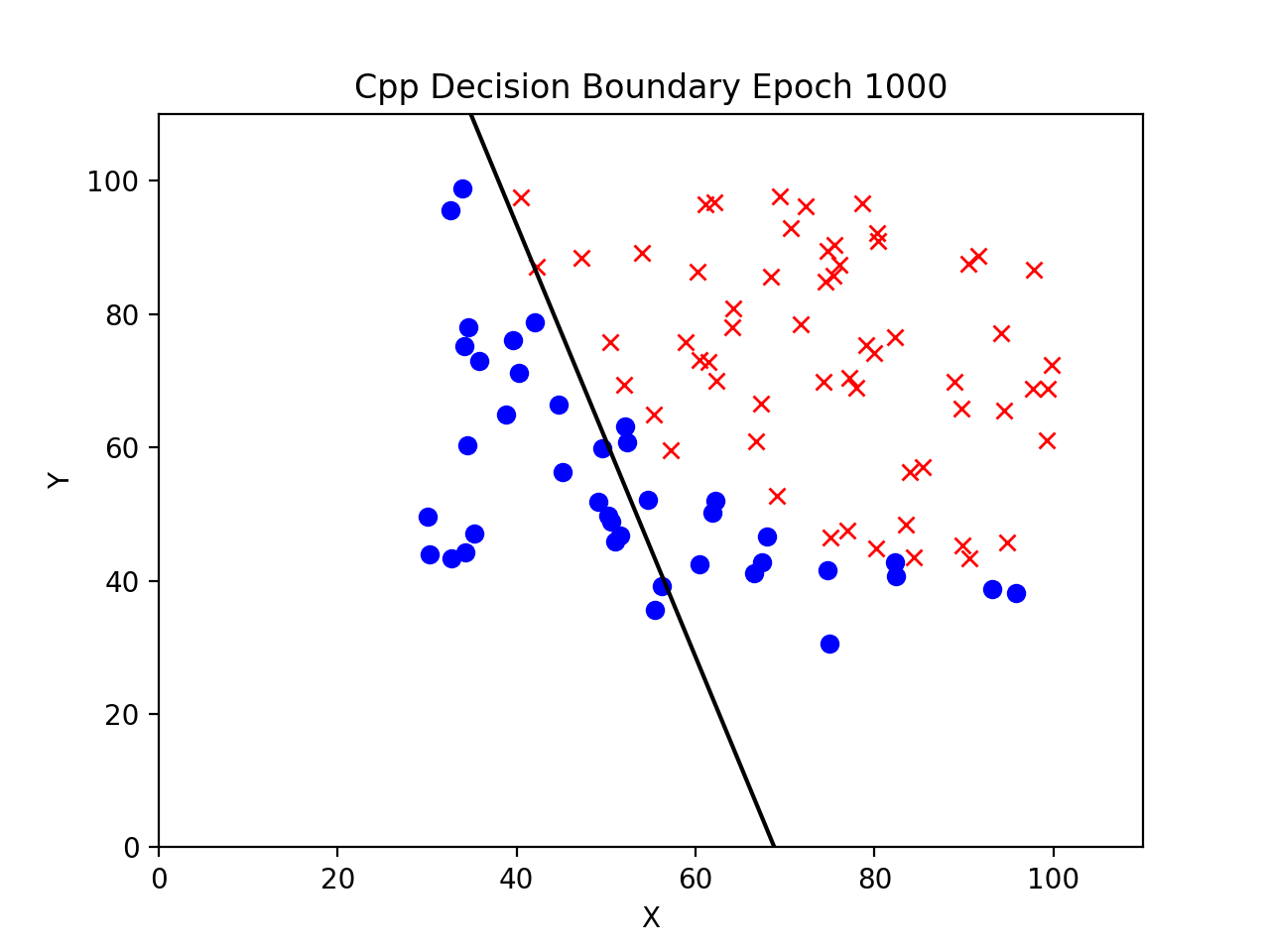
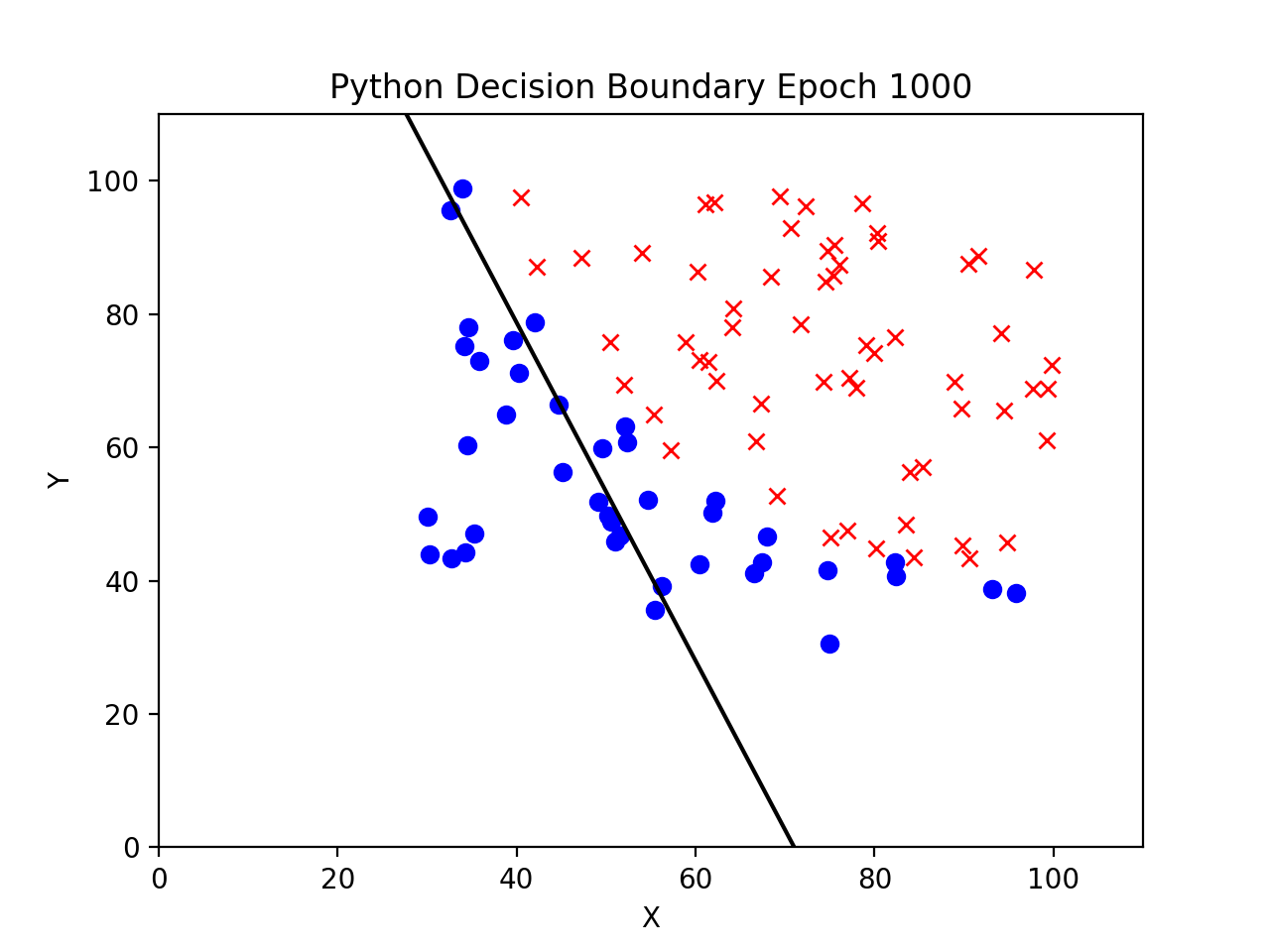
Decision Boundary at 25000 Epochs
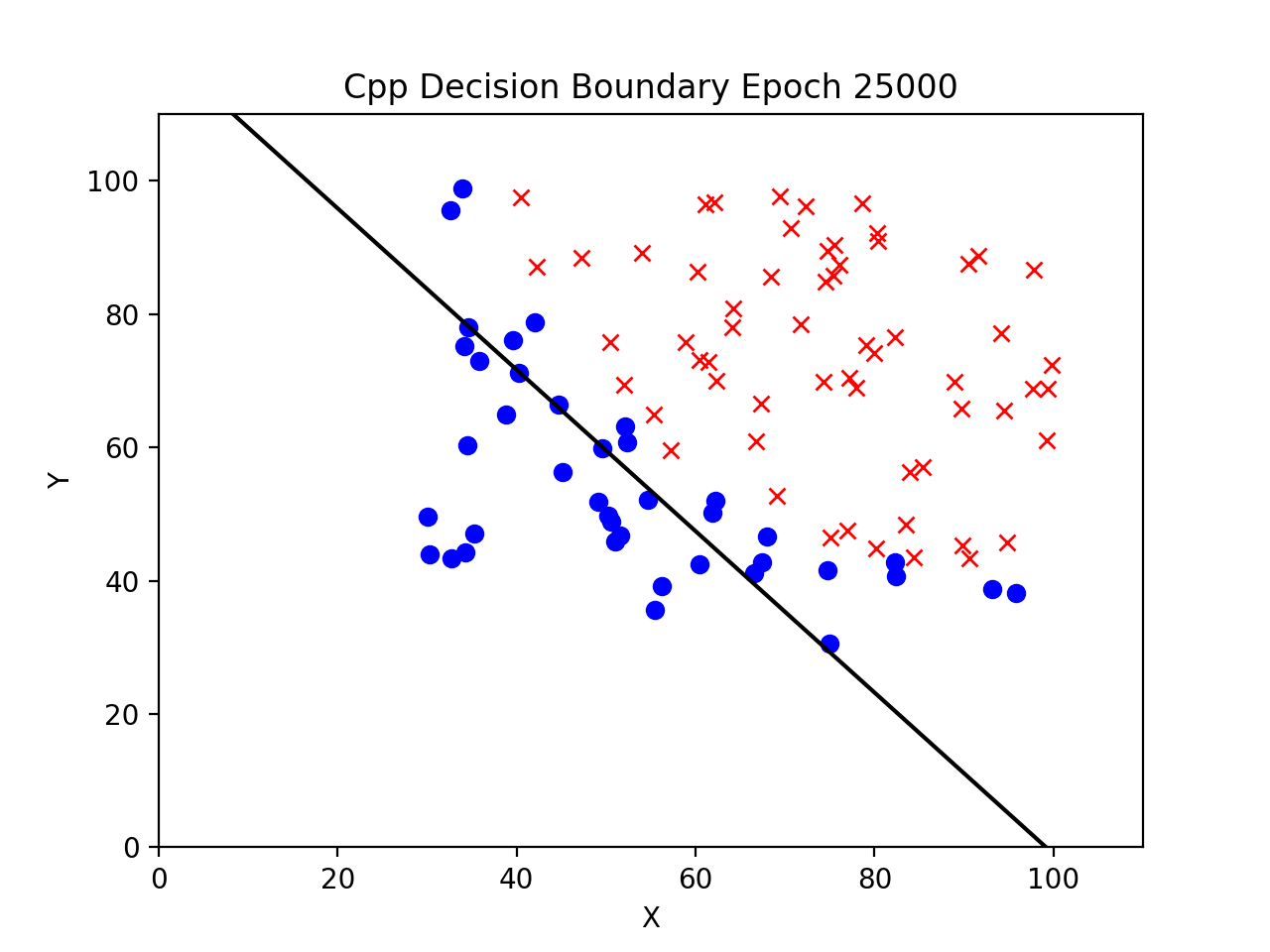
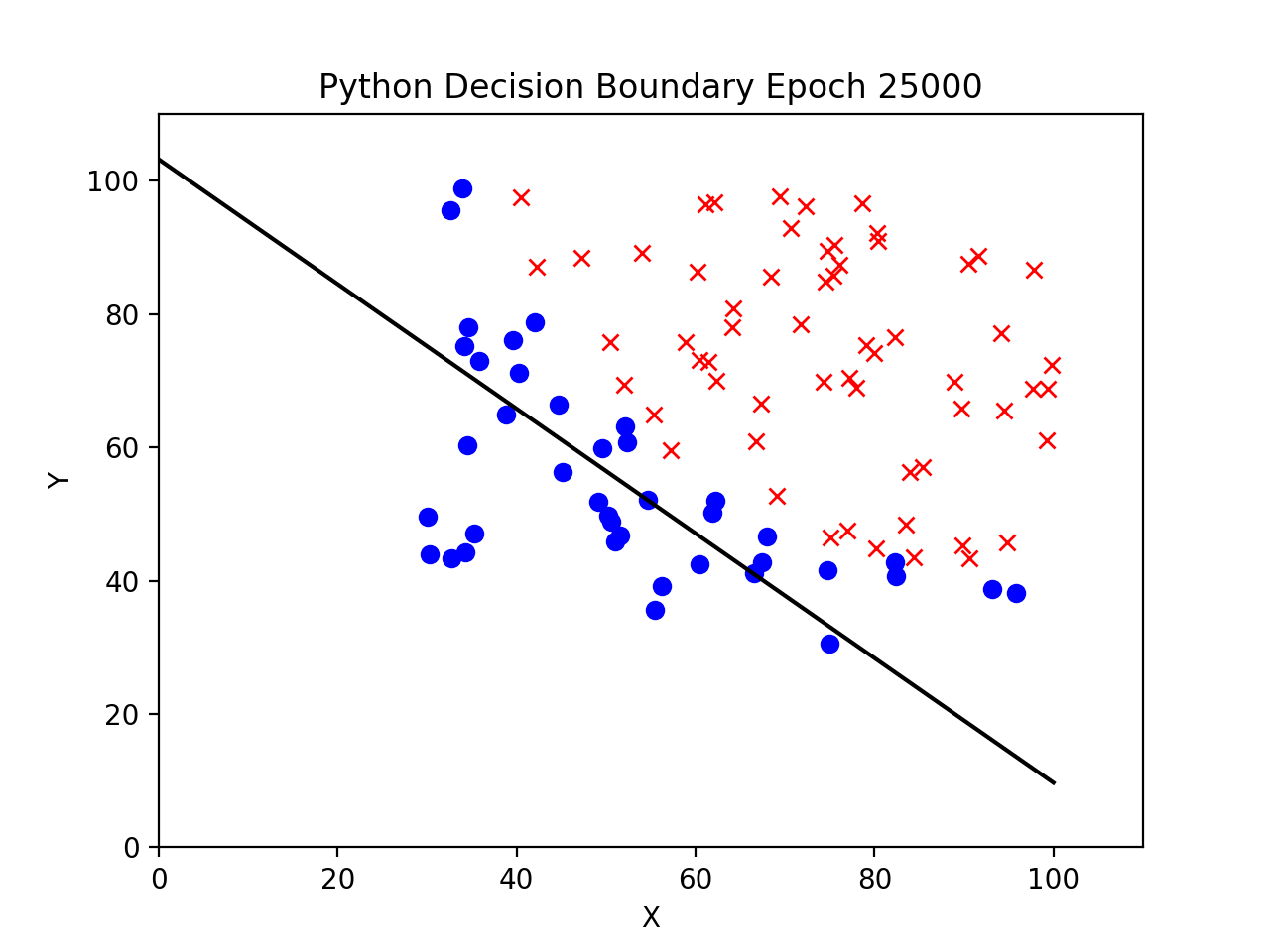
Decision Boundary at 50000 Epochs
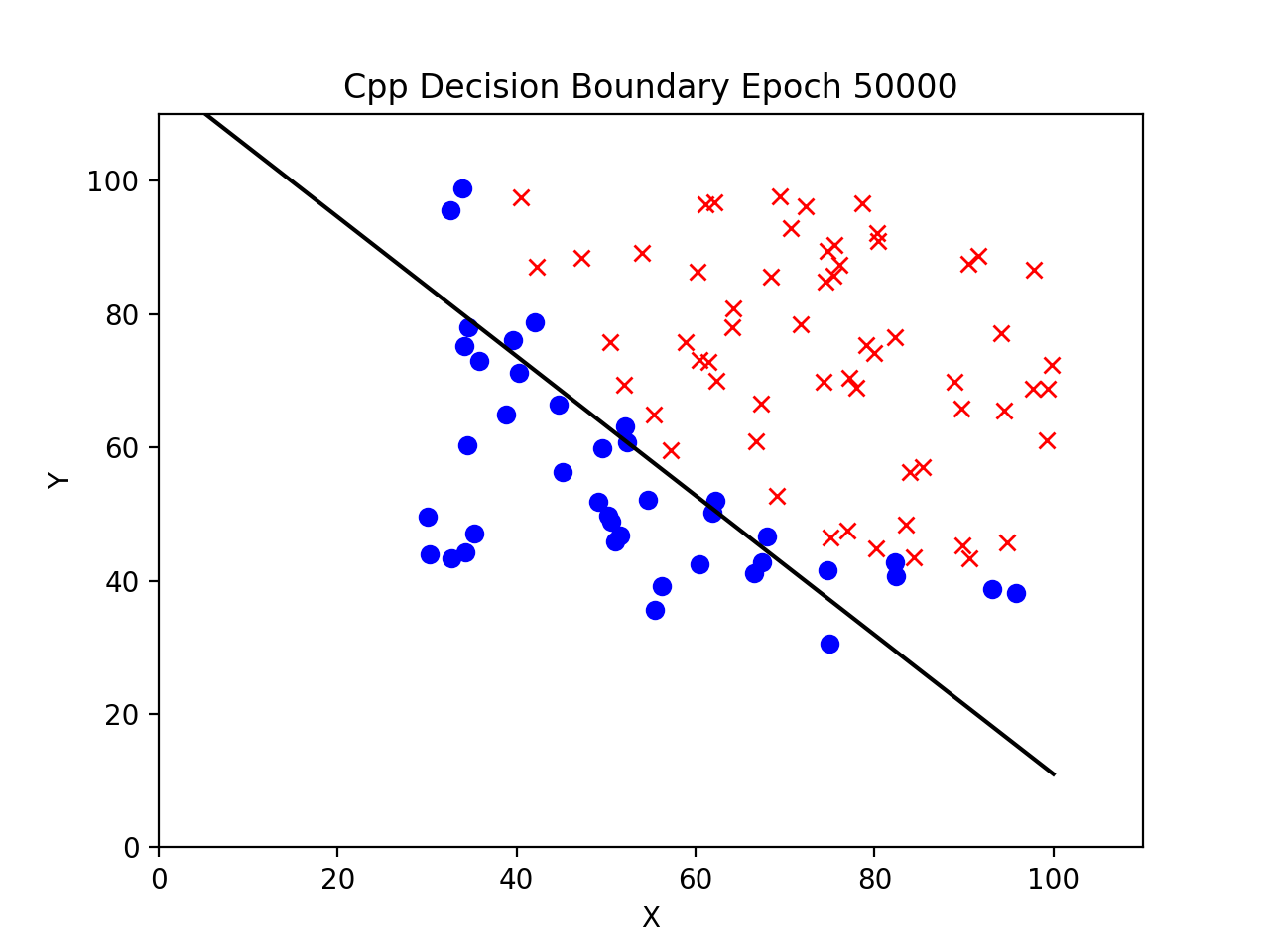
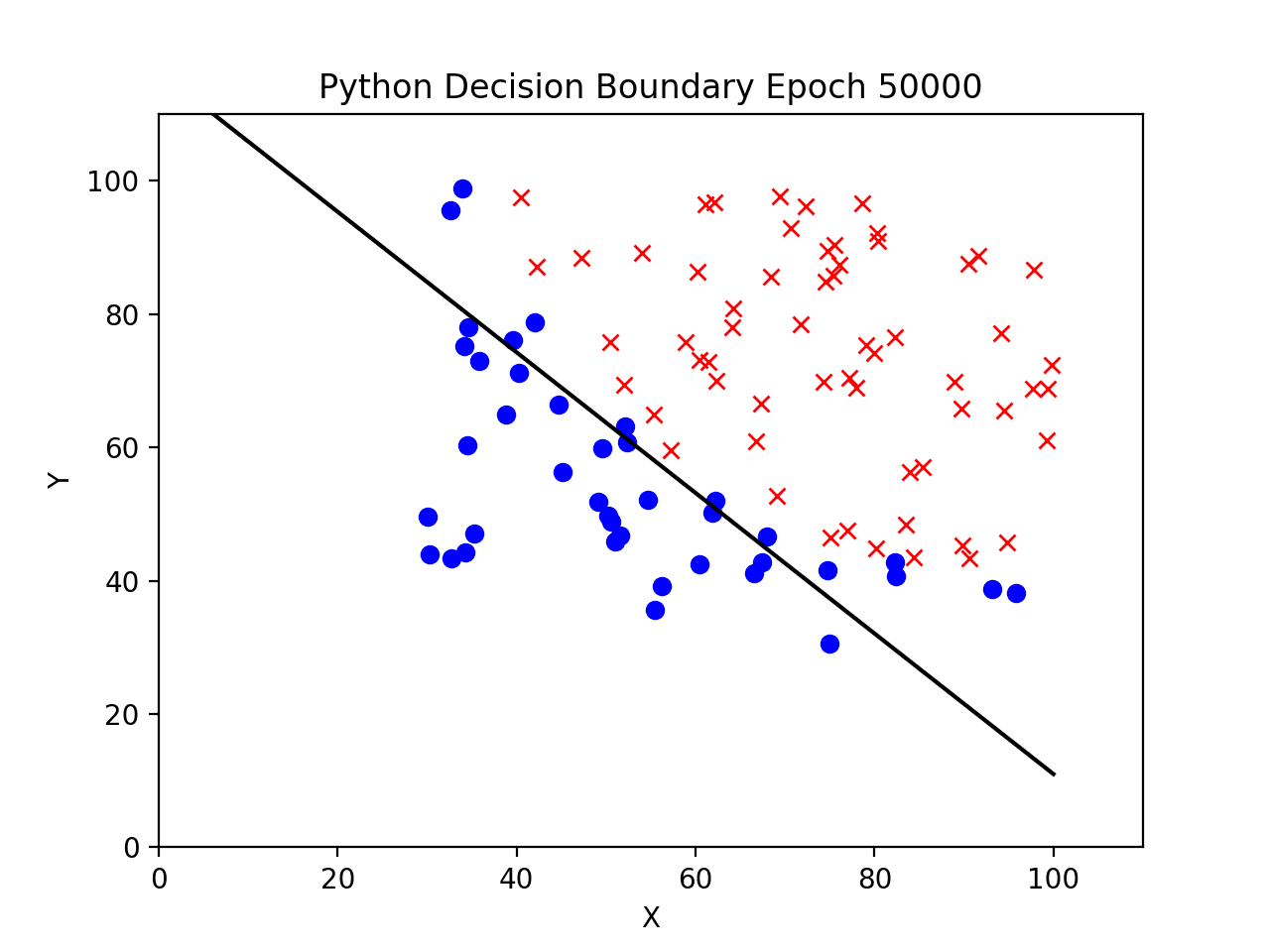
Summary
From the figures above, we see that the Perceptron algorithm implemented in C++ converges at a much faster rate than the same algorithm implemented in Python. A key reason is because Python loops are much slower than C++ loops. In addition, profiling the Python code reveals that numpy spends a significant amount of time on the insert function, which we use to add a bias to each input.